Внутри треугольника ABC взята произвольная точка O и через нее проведены три прямые,...

Question

Внутри треугольника ABC взята произвольная точка O и через нее проведены три прямые, параллельные сторонам треугольника. Эти прямые делят треугольник ABC на шесть частей, три из которых являются треугольниками. Радиусы окружностей, вписанных в эти треугольники, равны r1, r2 и r3. Найдите радиус окружности, вписанный в треугольник ABC.

Answer 1

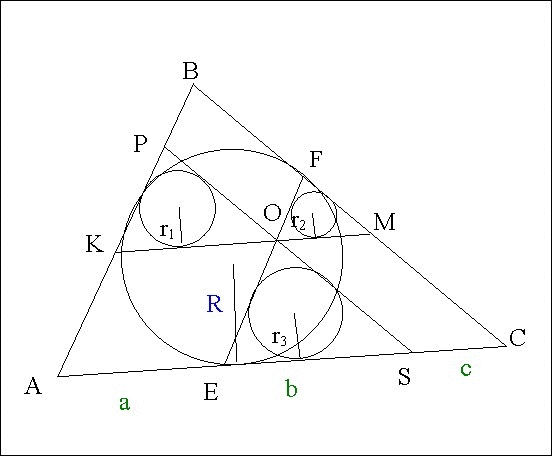
Дано: ∆АВС

EF║AB; PS║BC; KM║AC;

r₁; r₂; r₃ - радиусы вписанных окружностей в ∆KPO; ∆OFM; ∆EOS.

Найти R - радиус окружности, вписанной в ∆АВС

Решение.

1)  

Пусть

а - основание ∆KPO;

b - основание ∆EOS.

c - основание ∆OFM.

Но

а = КО = АЕ, как противоположные стороны параллелограмма АКОЕ.

с = ОМ = SC, как противоположные стороны параллелограмма SOMC.

Получаем

(a+b+c) - основание АС у ∆АВС.

2)

Все три внутренних треугольника подобны между собой и подобны данному ∆АВС, т.к. их соответственные стороны параллельны. 

В в подобных треугольниках соответствующие стороны и все соответствующие линии пропорциональны.

Из подобия следуют три пропорциональности:

а/(a+b+c)=r₁/R;

b/(a+b+c)=r₃/R;

c/(a+b+c)=r₂/R;

Сложим эти пропорции.

а/(a+b+c) + b/(a+b+c) + c/(a+b+c)= r₁/R + r₃/R + r₂/R;

(a+b+c)/(a+b+c) = (r₁+r₂+r₃)/R;

1 = (r₁+r₂+r₃)/R;

R = (r₁+r₂+r₃).

Ответ: R = r₁+r₂+r₃.

 

---

Comments

спасибо бро