В равнобедренной трапеции основания=4 и 6,а боковая сторона 5.Найдите сумму длинн...

Question

В равнобедренной трапеции основания=4 и 6,а боковая сторона 5.Найдите сумму длинн диагоналей.Помогите пожалуйста

Answer 1

проводим высоту и из этой же точки диагональ,

находим высоту корень из 25-1=24, 2 корня из 6

далее находим диагональ корень из 24+25=49, 7 сумма диагоналей 14

Answer 2

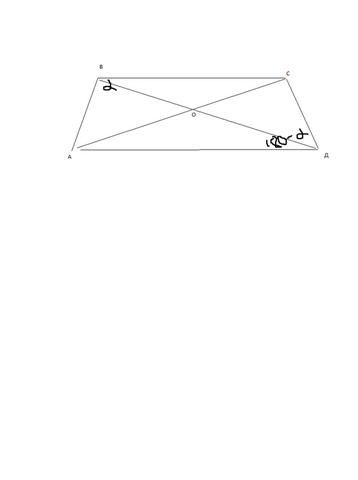
пусть угол АВс равен альфа, тогда АДС - 180-альфа. 

У тебя известны ВС=4, АВ=СД=5, АД=6. Тогда ты можешь по теореме косинусов найти диагонали а потом их сумму. Найдем сначала АС. АC^2=AB^2+BC^2-2AB*BC*cosальфа. И с другой стороны это равно СD^2+AD^2-2CD*AD*cos(180-альфа). 

Приравниваем. кос(180-альфа)=-косальфа. Этим пользуясь получается 4^2+5^2-2*4*5cosальфа=5^2+6^2+2*5*6cosальфа. 

cosальфа=-0.2. АС^2=4^2+5^2-2*4*5*(-0.2). AC^2=49, AC=7. Так же находишь вторую диагональ по теореме косинусов и складываешь. Скорей всего есть способ в несколько раз короче честно говоря) 

---