ДАНО
Y= 2x³ -3x²+1.
ИССЛЕДОВАНИЕ.
1. Область определения - D(x) - любое - Х∈(-∞;+∞) - функция непрерывная - разрывов нет.
2. Пересечение с осью У (это при Х=0)
Y(0) = 1.
2. Пересечение с осью Х - решение уравнения - Y(x)=0 (сложно и пока не
нужно).
3. Исследование на четность.
Y(-x) = -2*x³ - 3x² + 1 ≠ Y(x) - функция ни чётная ни нечётная (это опять сложно).
4. Поиск экстремумов - корней первой производной.
Y'(x) = 6x² - 6x = 6*x*(x-1) = 0
Два корня - х1 = 0 и х2 = 1. (Знак у параболы положительные - ветви вверх - отрицательная между корнями. Возрастает там, где производная положительная)
--(+)-------(0) ----(-)------(1)-------(+)
5. Возрастает - Х∈(-∞;0]∪[1;+∞)
Убывает - X∈[0;1].
6. локальные экстремумы.
Y(0) = 1 - максимум
Y(1) = 0 - минимум.
6. Точка перегиба в корне второй производной
Y"(x) = 12*x - 6 = 0 Коренеь - х = 6/12 = 0,5
7. Выпуклая - "горка" - Х∈(-∞;0,5)
Вогнутая - "ложка" - Х∈(0,5;+∞)
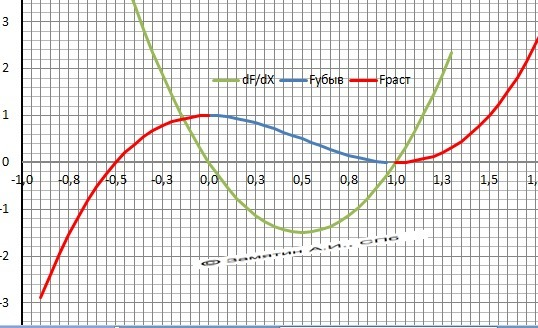
8. График в приложении.