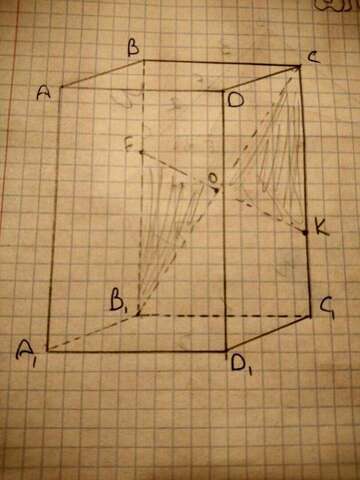
FO=OK - по условию. B1O=OC - по свойству параллелепипеда (точка пересечения диагонали с линией, вышедшей из ребра параллелепипеда делит диагональ пополам) угол СОК= углу В1ОF - как вертикальные. Соответственно, треугольник B1FO=треугольнику OCK - по двум равным сторонам и углу между ними. Что и требовалось доказать.