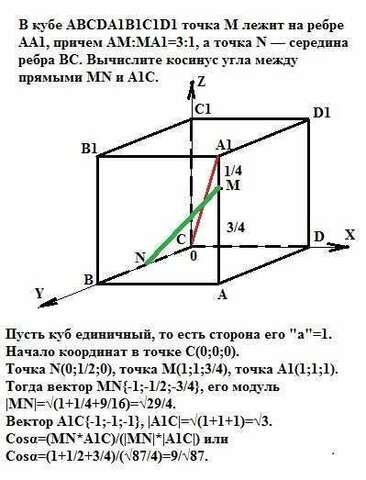
Для упрощения записей примем, что куб АВСDА1В1С1D1 - единичный, то есть его сторона равна 1.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.
Значит MN и A1C - скрещивающиеся прямые.
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем прямую СР параллельно прямой MN. Угол А1СР - искомый угол.
NA=√(АВ²+ВN²)=√(1+1/4)=√5/2 (по Пифагору).
NM=√(NA²+AM²)=√(5/4+9/16)=√29/4 (по Пифагору).
CP=NM=√29/4.
CA1=√(2+1)=√3 (диагональ куба).
А1Р=√(MA1²+MP²)=√(1/16+1/4)=√5/4.
По теореме косинусов:
Cosα=(CA1²+CP²-A1P²)/(2CA1*CP) или
Cosα=(3+29/16-5/16)/(2√3*√29/4)=(72/16)/(√87\2)=9/√87.
Ответ: Cosα=9/√87.
Второй вариант решения - координатный метод.
Пусть куб единичный, то есть сторона его "а"=1.
Начало координат в точке С(0;0;0).
Точка N(0;1/2;0), точка М(1;1;3/4), точка А1(1;1;1).
Тогда вектор MN{-1;-1/2;-3/4}, его модуль
|MN|=√(1+1/4+9/16)=√29/4.
Вектор А1С{-1;-1;-1}, |A1C|=√(1+1+1)=√3.
Cosα=(MN*A1C)/(|MN|*|A1C|) или
Cosα=(1+1/2+3/4)/(√87/4)=9/√87.
Ответ: Cosα=9/√87.