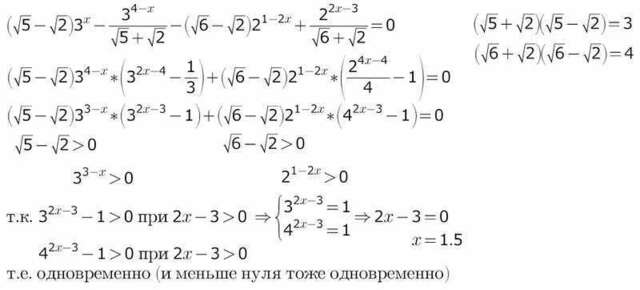В выражении присутствуют разные основания, следовательно,
либо нужно приводить к одному основанию (например, 3/4),
либо нужно приводить к одному показателю степени...
за скобки удобнее выносить основание в меньшей степени, потому
вынесла 3^(4-x) и 2^(1-2х) вместе с числовым множителем...
в обеих скобках осталась разность очень похожая одна на другую)))
а дальше рассуждения на тему: сумма двух неотрицательных чисел может быть равна нулю только в случае равенства нулю обоих слагаемых...
т.к. эти слагаемые одновременно положительны или одновременно отрицательны...
т.е. в уравнении корень один х=1.5
Ответ: 6х = 9