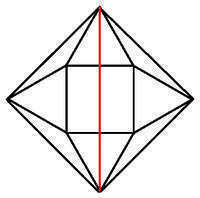
Четырехугольник, образованный вершинами равносторонних треугольников - квадрат (следует из симметрии построения).
Если сторона квадрата b, то диагональ b√2.
Диагональ образована двумя высотами равносторонних треугольников со стороной a и высотой квадрата со стороной a.
b√2 = 2*a√3/2 +a <=> b= a(1+√3)/√2 <=> b= a(√2+√6)/2
P2/P1= 4b/4a = (√2+√6)/2