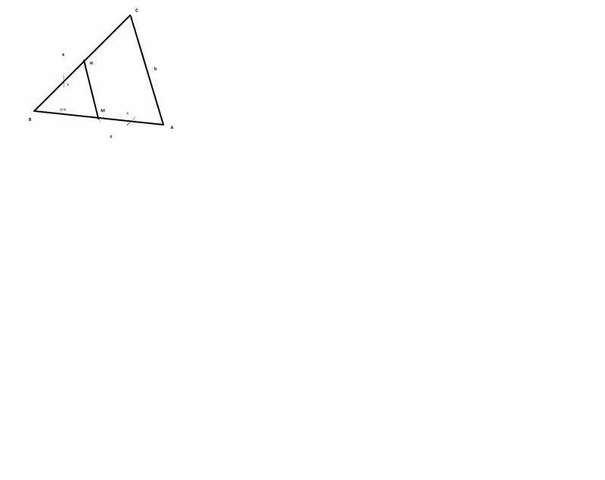
Понятно, что условие задачи написано "коряво", т.к. в таком контексте точки М и Н можно брать где угодно. Но с большой долей вероятности можно предположить, что точки М и Н лежат соответственно именно на сторонах АВ и ВС.
Смотрим рисунок и возвращаемся сюда же.
Треугольники АВС и МВН подобны, значит
МН/b=(c-x)/c=x/a ⇒ (1) MH/b=(c-x)/c (2) (c-x)/c=x/a
из (2) находим х. х=са/(с+а)
подставляем в (1)
МН=b(c-x)/c =b(c-ca/(c+a))/c
MH=bc/(c+a)