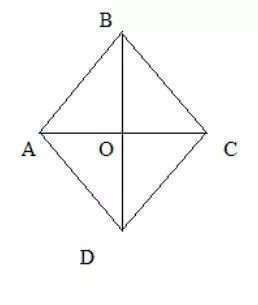
Дано: ABCD - ромб, BD=12кор(3)
Найти: P-?
уг. A=уг. C=120°
по свойсту диагонали ромба:
BO=1/2BD=6кор(3)
угол BOC - прямой(диагонали ромба пересекаются под прямыми углами).
В ромбе все стороны равны, значит:
P=4*a, где a - сторона.
треуг. BOC - прямоугольный.
т.к в ромбе диагонали являются биссектрисами его углов, то:
уг. BCO=1/2 уг. C=120/2=60°
следовательно угол OBC=180-90-60=30°
в прям. треуг. катет лежащий против угла 30°= 1/2 гипотенузы
т.к BC=a, то OC=1/2a
по теореме пифагора:
a^2=1/4a^2+BO^2
3/4a^2=6кор(3)^2
3/4a^2=36*3
3a^2=36*4*3
a^2=36*4
a=6*2=12
P=4*a=12*48
Ответ: 48