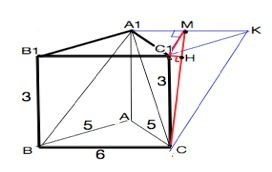
Достроим треугольник А1ВС до параллелограмма А1ВСК, т.к. С1 проецируется на его плоскость вне ∆ А1ВС
А1К параллельна и равна ВС и В1С1 ⇒
А1В1С1К - параллелограмм, А1С1 в нем диагональ;
треугольник А1С1К равнобедренный, А1М=КМ=3. С1М его высота. и равна 4 ( ∆ КМС1 - египетский, можно проверить по т.Пифагора).
По т.Пифагора СА1=√(СС1²+AC²)=√(9+25)=√34
Так как грани АВВ1А1 и АСС1А1 равны, то А1С=А1В=СК=√34
CM=√(CK²-MK*)=√(34-9)=5
Призма прямая, все ребра перпендикулярны основаниям, ⇒
СС1 перпендикулярен С1М, и ∆ МС1Спрямоугольный, его плоскость перпендикулярна плоскости А1КСВ.
Высота С1Н⊥МС ⇒перпендикулярна плоскости А1КСВ и является искомым расстоянием от точки С1 до плоскости А1ВС.
C1H=2S(CMC1):MC
2S (CМС1)=СС1•MC1=3•4=12
C1H=12/5