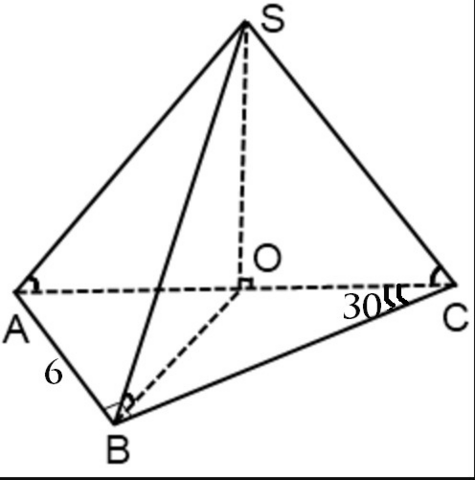
Если все боковые ребра наклонены под одним углом к основанию пирамиды, все боковые ребра равны, а вершина пирамиды проецируется в центр описанной около основания окружности. Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы, т.е. основанием высоты (SO = H) пирамиды явялется середина гипотенузы (AC) основания пирамиды.
1) B прямоугольном треугольнике ABC:
Катет AB = 6
Гипотенуза AC = 12
По теореме ПИфагора:
AC² = BC² + AB²
BC² = AC² - AB²
BC² = 12² - 6²
BC² = 108
BC = 6√3 (см)
Площадь основания пирамиды:
Sосн = 1/2 * AB * BC
Sосн = 1/2 * 6 * 6√3 = 18√3 (cм²)
В прямоугольном треугольнике SCO:
Катет СО = 1/2 AC
CO = 12 / 2 = 6 (cм)
∠SCO = 30°
Тангенсом ∠SCO является отношение противолежащего ему катета SO к прилежащему CO
tg(SCO) = SO / CO
SO = CO * tg(SCO)
SO =6 * tg 30° = 6 * 1/√3 = 6/√3 (см)
Объем пирамиды
V = 1/3 * Sосн * H 18√3 * 6
V = 1/3 * 18√3 * 6/√3 = ------------------ = 36 (см³)
3 * √3
-------------------------------------------------------------------------------------------------
2) В прямоугольном треугольнике ABC:
Гипотенуза AC = 12 (см)
∠ACB = 30°
Катет AB противолежит углу 30°, такой катет равен половине гипотенузы ⇒ AB = 6 (cм)
По теореме ПИфагора:
AC² = BC² + AB²
BC² = AC² - AB²
BC² = 12² - 6²
BC² = 108
BC = 6√3 (см)
Площадь основания пирамиды:
Sосн = 1/2 * AB * BC
Sосн = 1/2 * 6 * 6√3 = 18√3 (cм²)
В прямоугольном треугольнике SCO:
Катет СО = 1/2 AC
CO = 12 / 2 = 6 (cм)
∠SCO = 45°
∠CSO = 180 - 90 - 45 = 45 (°)
⇒ треугольник SCO - прямоугольный равнобедренный с основанием-гипотенузой и катетами-боковыми сторонами.
SO = CO = 6 (cм)
Объем пирамиды
V = 1/3 * Sосн * H
V = 1/3 * 18√3 * 6 = 6/3 * 18√3 = 36√3 (см³)