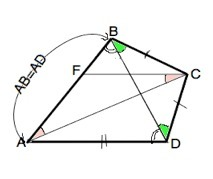
Проведем в данном четырехугольнике диагональ BD.
По услоию AF=FC, BC=CD, AB=AD ⇒
∆ АВD и ∆ ВСD - равнобедренные.
Рассмотрим треугольники АВС и АDС. Они равны по трем сторонам ( две по условию, сторона АС - общая)
Следовательно, ∠ВАС=∠DАС, ⇒ АС - биссектриса угла ВАD
В ∆ АFC стороны AF=CF, ∆ AFC – равнобедренный, ⇒ ∠FAC=∠FCA.
Но ∠ВАС=∠САD (из доказанного равенства ∆ АВС и ∆ АDС).
Из этого следует ∠FCA=∠CAD, а эти углы - накрестлежащие при пересечении FC и AD секущей АС.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти прямые параллельны. ⇒
FC||AD. Доказано.