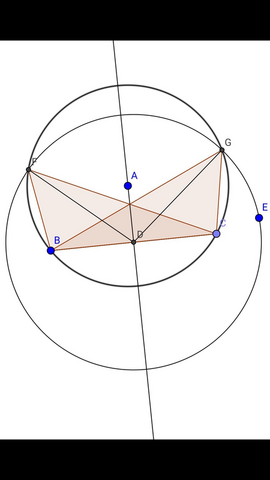
АВ - радиус описанной окружности, ВС - сторона треугольника, DE - медиана.
Построим окружность с радиусом АВ и хорду на ней, длиной ВС.
Из середины отрезка ВС, точки D, построим окружность с радиусом, равным медиане DE.
Точки пересечения двух окружностей F и G равноудалены от середины отрезка ВС.
DF=DG=DE - отрезки, равные медиане, значит треугольники ВСF и ВСG - искомые так как вписаны в окружность с радиусом АВ.