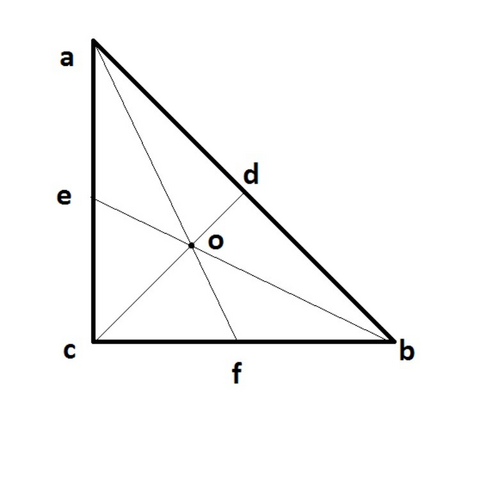
на чертеже треугольник abc. важно то что точка о является так называемым центром тяжести и делит медианы в отношении 2:1 начиная с вершины. т.е. ob/oe=2/1 следовательно oe=ob/2=10/2=5. так мы нашли нашу медиану be=oe+ob=10+5=15. рассмотрим треугольник ecb - он прямоугольный т.к. угол с=90 градусов. значит сторона ec вычисляется по теореме пифагора ec^2=be^2-cb^2. ec^2=15^2-12^2=225-144=81. ec=9. В свою очередь ec=ac/2 потому что сам отрезок ec получен изза разбиения медианой стороны ас надвое. т.е. ac=ec*2=18.
В общем-то катеты прямоугольного треугольника abc найдены, осталось по теореме пифагора найти гипотенузу ab. ab^2=ac^2+bc^2=324+144=468. ac=6*sqrt(13).