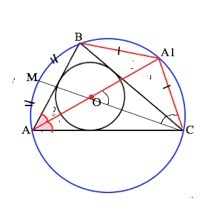
В треугольнике центр вписанной окружности лежит на пересечении биссектрис его углов.
АА1- биссектриса. ∠ВАА1=∠САА1. ⇒
В описанной вокруг ∆ АВС окружности вписанные ∠ВАА1 и ∠САА1 опираются на хорды, стягивающие равные дуги:
ВА1=СА1.
Проведем биссектрису СМ угла ВСА.
АА1 и СМ - хорды. Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
∠СОА1=(◡СА1+◡АМ):2
Вписанный угол равен половине градусной величины дуги, на которую опирается. ⇒
∠МСА1=( ◡МВ+◡ВА1):2
◡МВ=◡АМ ( т.к. ∠ВСМ=∠АСМ).
◡ВА1=◡СА1 как дуги, на которые опираются равные ∠ВАА1 и ∠САА1
Следовательно, (◡СА1+◡АМ):2=(◡МВ+◡ВА1):2
Отсюда следует равенство ∠СОА1=∠ОСА1, ⇒
∆ ОА1С - равнобедренный, ⇒ОА1=А1С
Отрезки ВА1=СА1=ОА1. Доказано.