. в трапеции АВСD на большем основании АD
отмечена точка М так что АМ=3 см. СМ=2 см,
∠ ВАD=∠ ВСМ. Найдите длины сторон АВ и ВС
Так как ∠ ВАD=∠ ВСМ, то ∠В=180° -∠ А, ∠D=180°-∠ С, и ∠В=∠D.
В четырехугольнике АВСМ противоположные углы равны. Получися параллелограмм АВСМ. ВС=АМ=3, АВ=СМ=2
--------------------------
2.
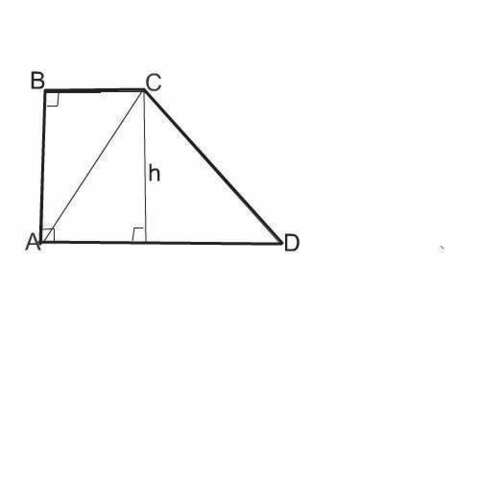
Sᐃ АСD= h∙AD:2
Высота h ᐃ АСD=АВ=8 см
AD=BC+ √(CD²- h²)=√(100 - 64)=√36=4+6 =10cм
S ᐃ АСD= 8∙10:2=40 см²
S трапеции АВСD=h∙( AD+ВС):2=8∙(10+4):2=56 см²
-------------------------------------
3.
Так как ∠ВDА= углу, под которым МК пересекает ВD,
МК║АС ⇒ ∠ВМК=∠ВАС, ∠ВКМ=∠ВСА ∠В - общий в треугольниках АВС и МВК.
ᐃ ВМК~ᐃ АВС
Из подобия треугольников ⇒,
АВ:ВМ=ВС:ВК
Примем МА=х, тогда
(х+7):7=27:9
9х=126
х=14см
АВ=7+13=21 см
Коэффициент подобия треугольников 21:7=3
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия. S ᐃ АВС: S ᐃ ВМК=3²:1=9:1
----------------------------
4.
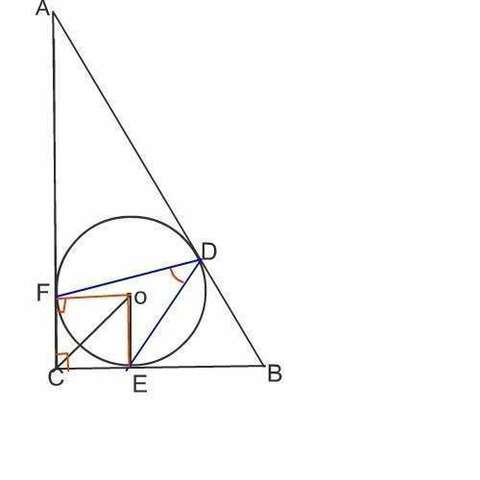
Соединим центр вписанной окружности с точками касания.
Получим квадрат CFOE с диагональю СО. Так как СО=2√2, то стороны квадрата равны 2, и радиус окружности
r = 2.
∠ ЕОF, как угол квадрата, равен 90°
∠ FDE как вписанный, равен половине центрального ∠FOE и равен 45°