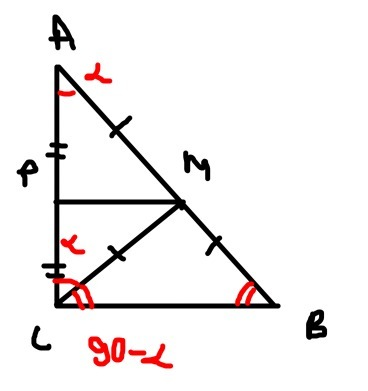
Прямая РМ является серединным перпендикуляром по отношению а к отрезку АС. Так как прямая РМ проходит через середину данного отрезка , и перпендикулярна ему.
Любая точка , лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
Следовательно, отрезок СМ равен отрезку АМ ⇒ АМ=13 см.
Теперь найдем отрезок МВ.
Треугольник СМВ равнобедренный . Пусть угол ∠А=α, поскольку треугольник АМС равнобедренный , то угол РСМ тоже равен α. Но сумма острых углов в прямоугольном треугольнике равна 90°, и угол МСВ=90-α
, но угол МВС тоже равен 90°-α ⇒ Треугольник МСВ равнобедренный, и его боковые стороны равны 13 см.
Гипотенуза равна сумме двух этих отрезков АВ=АМ+МВ=13*2=26