Две окружности пересекаются в точках C и D. Точка B — центр второй окружности, а отрезок...

Question

40 просмотров

Две окружности пересекаются в точках C и D. Точка B — центр второй окружности, а отрезок AB — диаметр первой. Из точки C провели касательную к первой окружности, которая пересекает вторую окружность в точке E, отличной от C. Найдите радиус первой окружности, если радиус второй равен 15, а длина отрезка CE равна 18.

Геометрия Wowalion_zn (1.4k баллов) 12 Май, 18 | 40 просмотров

Дано ответов: 2

Правильный ответ

Пусть O - центр первой окружности, R - ее радиус. ∠ECB=∠DCB=α, так как первый - это угол между касательной CE и хордой CB первой окружности, он измеряется дугой CB первой окружности, а второй угол - вписанный и опирается на дугу BD первой окружности. То, что дуги BC и BD равны, думаю, вопросов не вызывает. Из ΔEBC с известными сторонами CE=18 и BC=BE=r=15 находим ∠ECB=α: (CE/2)/BC=cos α; cos α=0,6 (⇒sin α=0,8).

Остается применить теорему синусов к первой окружности:
DB=r=2Rsinα; R=r/(2sin α)= 9,375

Ответ: 9,375

yugolovin_zn (64.0k баллов) 12 Май, 18

То, что дуги BC и BD равны, вопросов не вызывает. Речь идет о несоответствии РИСУНКА условию задачи. По этому рисунку найденный радиус МЕНЬШЕ, чем отрезок, в него ВХОДЯЩИЙ. То есть составители задач берут какую-то верную задачу и начинают тиражировать ее с другими данными, предлагая готовые рисунки якобы для облегчения решения, не задумываясь о том, что не проверенные данные могут запутать решающего: http://prntscr.com/ehqe5w

оставил комментарий Andr1806_zn (117k баллов) 12 Май, 18

Andr1806_zn · Answer 1 · 2018-05-12T08:13:30+0000

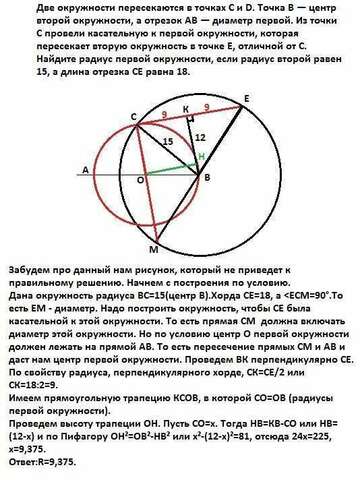
Первый вариант. Поскольку данный в условии рисунок ввел меня в заблуждение,
начнем с построения по условию.
Пусть дана окружность радиуса R=ВС=15(центр В). Хорда СЕ=18,
а То есть прямая СМ должна включать диаметр этой окружности. Но по условию центр О первой окружности должен лежать на прямой АВ.
То есть пересечение прямых СМ и АВ и даст нам центр первой окружности. Проведем ВК перпендикулярно СЕ. По свойству радиуса, перпендикулярного хорде, СК=СЕ/2 или СК=18:2=9.
Имеем прямоугольную трапецию КСОВ, в которой СО=ОВ (радиусы первой окружности).
Проведем высоту трапеции ОН. Пусть СО=х. Тогда НВ=КВ-СО или НВ=(12-х) и по Пифагору ОН²=ОВ²-НВ² или х²-(12-х)²=81,
отсюда 24х=225, х=9,375.
Ответ:R=9,375.

Второй вариант:
При внимательном рассмотрении оказалось, что можно решить и с приведенным в условии рисунком.
Смотрите второе приложение.
Проведем ВК перпендикулярно СЕ.
По пифагору ВК=√(ВС²-СК²) или ВК=√(225-61)=12.
Прямоугольная трапеция СКВО, в которой Проведем высоту ВН трапеции.
ВН=СК=9.
ОВ=ОС=х (искомый радиус).
Тогда по Пифагору из треугольника ОНВ:
(х-12)²+9²=х².
х²-24х+144+81=х².
-24х+225=0.
24х=225.
х=225/24=9,375.
Ответ: R=9,375.