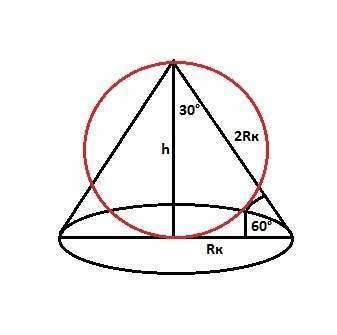
Если имелось в виду: "Высота конуса и диаметр шара равны",
то решение такое:
Радиус основания конуса равен половине длины образующей конуса,
так как лежит напротив угла 30° (из треугольника сечения)
Тогда 4Rк²-Rк²=h² и 3Rк²=h²
То есть Rк=h*/√3.
Площадь основания конуса So=π(Rк)² или So=πh²/3.
Объем конуса равен
Vк=(1/3)*So*h или Vк=(1/3)*(1/3)πh³= πh³/9.
Rш=h/2 (дано).
Vш=(4/3)πRш³ или Vш=(4/3)πh³/8.
Vк/Vш=(πh³/9)/((4/3)πh³/8)=(πh³*3*8)/(9*4*πh³)=2/3. Это ответ.