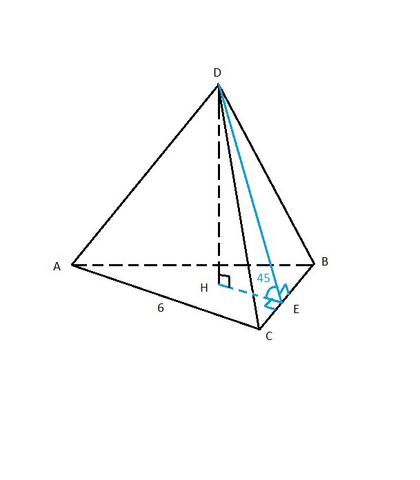
1)

2) Опустим высоту DE в грани DCB. Т.к. пирамида правильная ⇒ ΔDCB равнобедренный ⇒ DE - медиана ⇒ E - середина ребра CB.
Соединим AE. т.к. ΔABC - равносторонний ⇒ AE медиана и высота.
DE ⊥ CB и AE ⊥ CB ⇒ ∠AED - линейный угол двугранного угла.
3) Опустим высоту DH. т.к. пирамида правильная H делит AE в отношении 2:1 начиная от вершины ⇒ HE = 1/3 AE.
ΔDHE - прямоугольный и равнобедренный ⇒ h = DH = HE = 1/3 AE;


4)