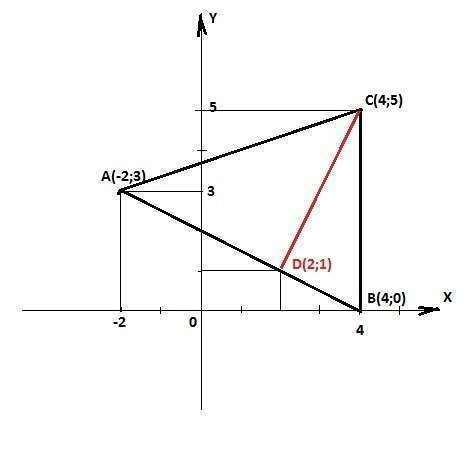
Уравнение прямой АВ - это уравнение прямой, проходящей через точки
А(-2;3) и В(4;0)
(X-Xa)/(Xс-Xa)=(Y-Ya)/(Yс-Ya) или
(X+2)/6=(Y-3)/(-3) => 3x+6y-12=0
Общее уравнение прямой АС имеет вид: Аx+Вy+С=0
В нашем случае уравнение прямой АС имеет коэффициенты:
А=3, В=6 и С=-12.
Из уравнения прямой АВ «снимаем» вектор нормали: n(3;6), который и будет направляющим вектором прямой СD (перпендикуляра к АВ).
Уравнение прямой СD составим по точке С(4;5) и направляющему вектору n(3;6):
(x-4)/3=(y-5)/6 или 6x-3y-9=0 или 2х-y-3=0.
Нам дано, что координаты точки D(x=2y;y).
Решаем систему двух уравнений подстановкой.
Получаем, что точка D(2;1).
Тогда высота |СD|=√[(2-4)²+(1-5)²]=√(4+16)=2√5.
Ответ:CD=2√5.