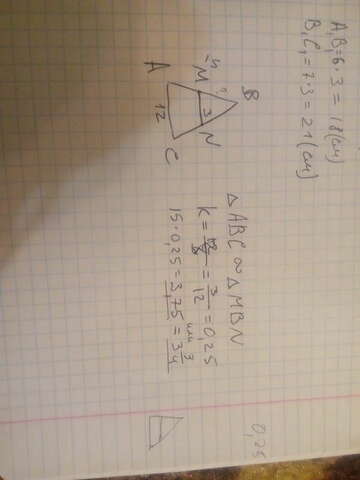Всё просто рассмотрим два треугольника АВС и MBN, так как их углы равны, то их можно считать подобными(~)
(тут поподробнее, почему же углы те же:
при пересечении двух параллельных прямых третей прямой образуется восемь различных углов, в данном случае мы рассматриваем два из них, а именно соответственные углы( углы ВМN и BAC, а так же углы BNM и BCA), которые, в свою очередь, попарно равны. Так что мы имеем два подобных треугольника.)
теперь рассчитываем коэффициент подобия: бОльшую сторону треугольника MBN делим на бОльшую сторону треугольника АВС, получаем 0.25.
Теперь умножаем сторону АВ на коэффициент подобия и получаем сторону меньшего треугольника.
Фото с решением приложил.