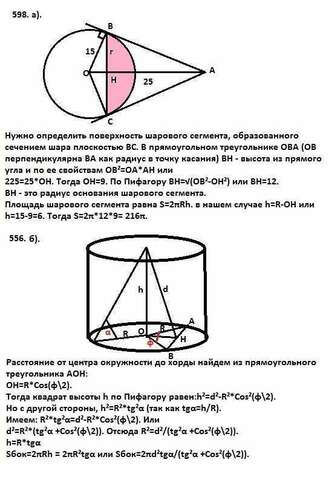
598 а). Нужно определить поверхность шарового сегмента, образованного сечением шара плоскостью ВС (смотри рисунок).
В прямоугольном треугольнике ОВА (ОВ перпендикулярна ВА как радиус в точку касания) ВН - высота из прямого угла и по ее свойствам ОВ²=ОА*АН или 225=25*ОН.
Тогда ОН=9. По Пифагору ВН=√(ОВ²-ОН²) или ВН=12.
ВН - это радиус основания шарового сегмента.
Площадь шарового сегмента равна S=2πRh. в нашем случае h=R-ОН или h=15-9=6.
Тогда S=2π*12*9= 216π.
556 b). Расстояние от центра окружности до хорды найдем из прямоугольного треугольника АОН (смотри рисунок):
ОН=R*Cos(φ\2).
Тогда квадрат высоты h по Пифагору равен:h²=d²-R²*Cos²(φ\2).
Но с другой стороны, h²=R²*tg²α (так как tgα=h/R).
Имеем: R²*tg²α=d²-R²*Cos²(φ\2). Или
d²=R²*(tg²α +Cos²(φ\2)). Отсюда R²=d²/(tg²α +Cos²(φ\2)).
h=R*tgα.
Sбок=2πRh = 2πR²tgα или
Sбок=2πd²tgα/(tg²α+Cos²(φ\2)).