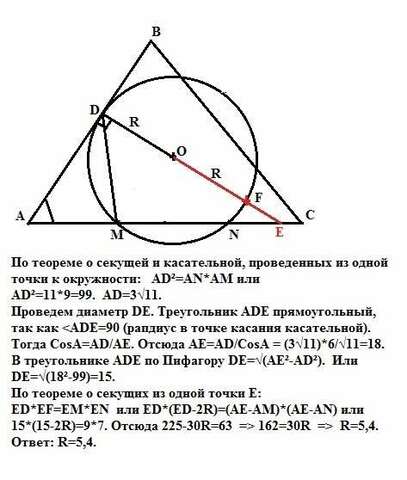
По теореме о секущей и касательной, проведенных из одной точки к окружности: AD²=AN*AM или
AD²=11*9=99. AD=3√11.
Проведем диаметр DE. Треугольник ADE прямоугольный, так как Тогда CosA=AD/AE. Отсюда АЕ=AD/CosA = (3√11)*6/√11=18.
В треугольнике ADE по Пифагору DE=√(AE²-AD²). Или
DE=√(18²-99)=15.
По теореме о секущих из одной точки Е:
ED*EF=EM*EN или ED*(ED-2R)=(AE-AM)*(AE-AN) или
15*(15-2R)=9*7. Отсюда 225-30R=63 => 162=30R => R=5,4.
Ответ: R=5,4.