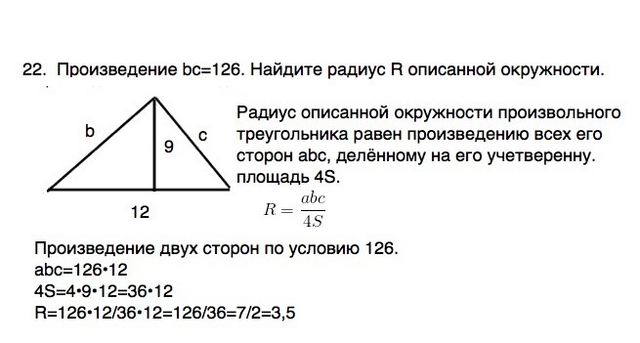
Сторона треугольника равна 12, высота, проведенная к этой стороне, равна 9, а произведение двух других сторон равно 126. Найти радиус описанной окружности.
Радиус описанной окружности произвольного треугольника равен произведению его сторон abc, делённому на его учетверенную. площадь 4S.
R=abc/4S
Произведение ab по условию 126.
abc=126•12
4S=4•9•12=36•12
R=126•12/36•12=126/36=7/2=3,5 (ед.площади)