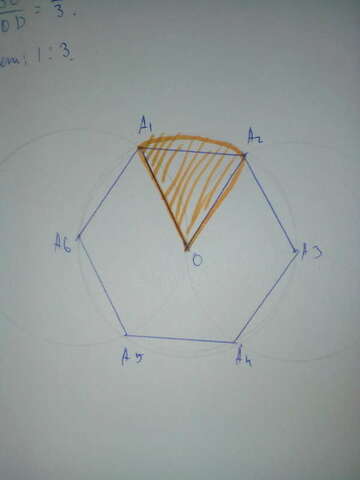
Найдём градусную меру центрального угла:
Исходя из того, что опираться он будет на дугу описанной окружности, каждый угол шестиугольника равен 120°, а радиусы являются биссектрисами его углов, получаем:
180° - 120°/2 - 120°/2 = 180° - 60° - 60° = 60°.
Площадь кругового сектора находится по формуле:
Sсек = πr²A/360°
A = 60°.
Значит, Sсек = 1/6Sокруж
Sокр. = 6Sсек = 6•6π = 36π.
Радиус описанной окружности тогда равен √Sокр/π = 6.
Радиус описанной окружности равен стороне шестиугольника.
Радиус вписанной окружности равен:
r = R√3/2 = 6√3/2 = 3√3.
Площадь любого описанного многоугольника находится по формуле:
S = 1/2Pr
Sшест. = 1/2•6a•3√3 = 1/2•6•6•3√3 = 54√3.