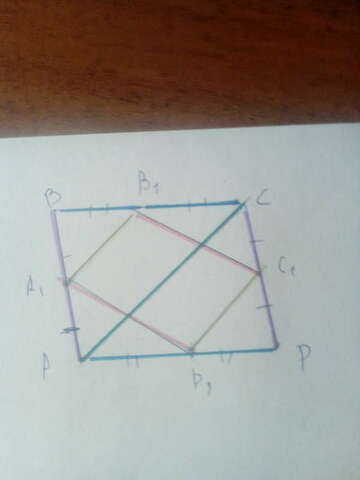
Проведем диагональ АС.
Т.к. все вершины четырёхугольника являются серкдинами сторон данного параллелограмма, то данный четырёхугольник тоже будет являться параллелограммом (теорема Вариньона).
Рассмотрим ∆A1BB1 и ∆ABC.
Т.к. AA1 = A1B, BB1 = B1C, то A1B1 - средняя линия. Тогда ∆A1BB1 ~ ∆ABC => SA1BB1/SABC = (BB1/BC) = 1/4.
SABC = SADC, т.к. ∆ABC = ∆ADC => SABC = 1/2SABCD = 10 см².
Тогда SA1BB1 = 1/4•10 см² = 2,5 см².
SA1BB1 = SB1CC1 = SC1DD1 = SA1AD1, т.к. все эти треугольники равны довш другу по двум сторонам и углу между ними.
Тогда SA1B1C1D1 = SABCD - 4SA1BB1 = 20 см² - 10 см² = 10 см².
Ответ: 10 см².