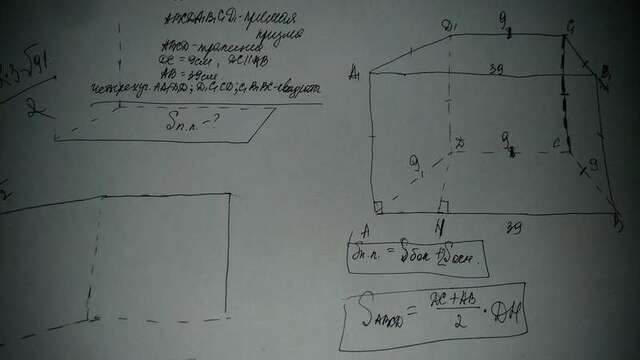
Так як AA1 = DD1 = A1D1 = AD => DD1 = AA1 = CC1 = BB1 (призма пряма) => що всі квадрати рівні між собою і AD = DC = CB, A1D1 = D1C1 = C1B1 = 9 см. Отже, всі сторони даних квадратів по 9 см. Sadcd = S a1b1c1d1:DH перпендикулярно AB, AH = AB-DC = 39-9 = 30 см. Трикутник AHD: по теоремі Піфагора: DH² = 30²-9², DH² = (30-9) (30 + 9), DH² = 3 * 7 * 3 * 13, DH = 3√91. Sadcd = (48 * 3√91) / 2 = 72√91 (див в квадраті) = S a1b1c1d1. S підстави = 2 * 72√91 = 144√91. S бічна = 3 * S a1add1 + S aa1b1b. S бічна = 3 * 81 + 9 * 39 = 594. S повну поверхню = 594 + 144√91. Перевір ще раз