ДАНО
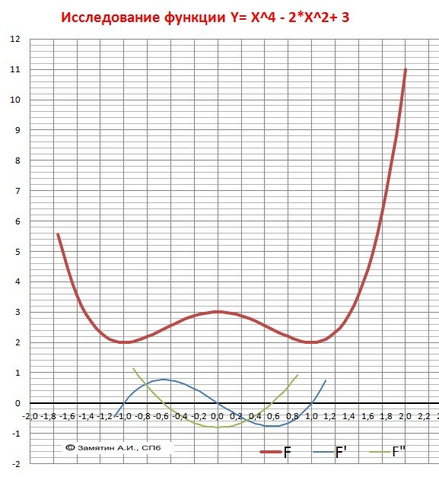
Y = X⁴ - 2*X² + 3
НАЙТИ
Экстремумы в интервале [0,2]
РЕШЕНИЕ
Для поиска экстремумов нужно найти корни первой производной.
Y' = 4*X³ - 4*X = 4*X*(X²- 1)
Корни производной
х1 = 0 - максимум
и два корня уравнения Х² - 1 =0
х2 = 1 - минимум и (х3 = - 1 х3 - исключаем - вне интервала.)
Наименьшее значение функции
У(1) = 2 - ОТВЕТ
Наибольшее значение
У(2) = 11 - ОТВЕТ
Дополнительно - график прилагается..