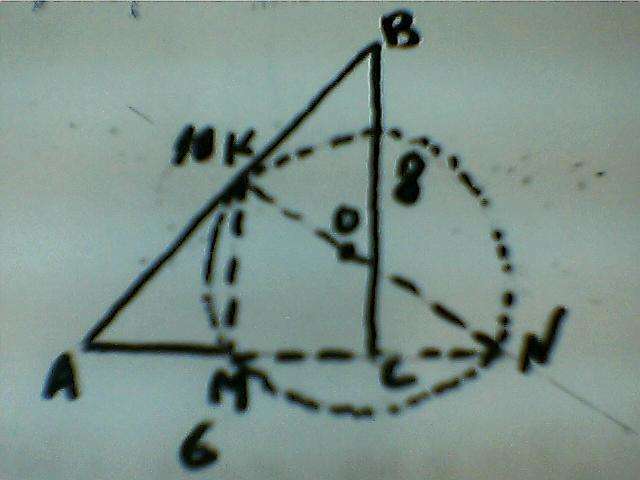Катеты прямоугольного треугольника равны 6 и 8. Через середину меньшего катета и середину...

Question

Катеты прямоугольного треугольника равны 6 и 8. Через середину меньшего катета и середину гипотенузы проведена окружность, касающаяся гипотенузы. Найти радиус окружности.

Comments

Касается в этой самой середине гипотенузы ( = 10). Центр лежит на перпендикуляре из середины гипотенузы. Средняя линяя, которая II большему катету и равна 4 - это хорда окружности и сторона вписанного в окружность прямоугольного треугольника, подобного исходному (там равные углы), то есть египетского. Коэффициент подобия 4/6, значит диаметр 10*4/6; радиус в 2 раза меньше. 10/3;

---

извините отошел

---

здесь уже решили

---

красивое решение

Answer 1

Рисунок см. во вложении. Все предыдущий автор верно описал. Просто небольшие пояснения. При продолжении меньшего катета АС до пересечения с окружностью получим точку N, причем КN - диаметр, т.к. угол КМN - прямой (KM||BC, как средняя линия). Вот и получился прям-ый тр-ик KMN, вписанный в окружность, подобный исходному, т.к угол NKM = углу ВАС( у них взаимно перпендикулярны стороны). Гипотенуза исходного тр-ка АВ=10 (по т. Пифагора), пусть KN = d - диаметр окр-ти, КМ = 4, как ср. линия исходного тр-ка.
Теперь можно составить пропорцию:
d/AB = KM/AC, или d/10 = 4/6
Отсюда:d = 20/3, а радиус: R = 10/3

---