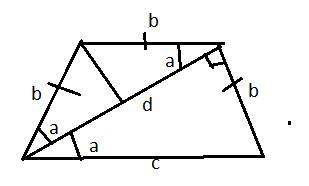
Ответ: с/b = 2
Объяснение:
В равнобедренном треугольнике углы при основании равны, пусть это угол а. тогда и диагональ является биссектрисой острого угла, так как острые углы с нижним основанием и верхним основанием равны, как накрест лежащие при параллельных основаниях. То есть угол между нижним основанием и диагональю тоже равен а.
Проведем высоту (она же медиана и биссектриса) равнобедренного треугольника к диагонали и из получившегося прямоугольного треугольника cosa = d/2:b=d/2b, где b боковая сторона. Из прямоугольного треугольника cosa=d/c, где с длина нижнего основания. Приравняв правые части этих уравнений получаем
d/2b=d/c и отсюда с/b= 2