ДАНО
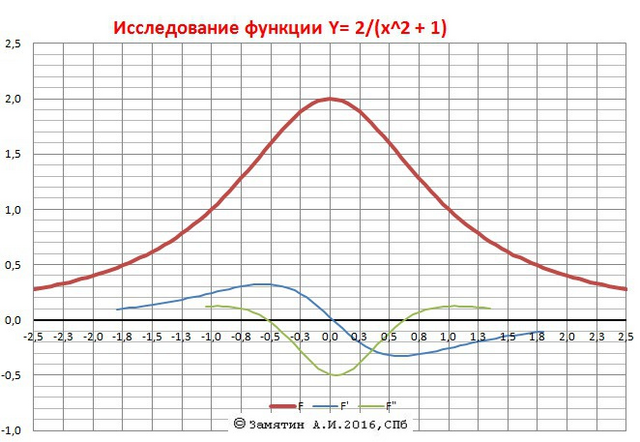
Y = 2/(x²+1)
ИССЛЕДОВАНИЕ
1. Область определения. Х∈(-∞,+∞).
2. Пересечение с осью Х - нет. Х∈∅.
3. Пересечение с осью У. Х=0, У(0) = 2.
4. Поведение на бесконечности.
У(-∞) = 0, У(+∞) = 0.
5. Исследование на четность.
У(-х) = - У(х) - функция четная.
6. Поиск экстремумов по первой производной.
Y' = -4x/(x²+1)² =
Нули производной при Х = +/- 1.
Минимум - Ymin(-1) = -1
Максимум - Ymax(1) = 1.
7. Возрастает - Х∈(-∞,0]
Убывает - X∞[0,+∞)
8. Точки перегиба по второй производной.

12x²-4 = 0
x = +/- √3/3 ~ 0.58
9. Асимптота . F(∞) = Y(x)/x = 0.
10. График прилагается.