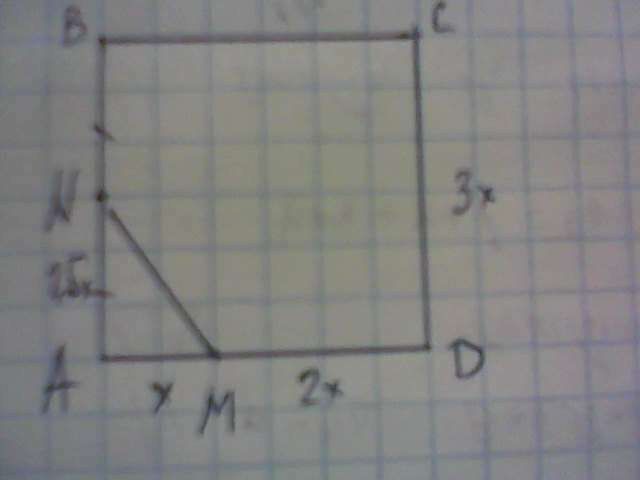
См фото.
Пусть АМ=х, МD=2х, сторона квадрата АВ=3х.
Площадь квадрата равна S1=3х·3х=9х².
Площадь треугольника АNМ равна S2=0,5·1,5х·х=0,75х².
Найдем отношение площадей S1/S2=0,75х²/9х²=1/12.
Ответ: S1 составляет одну двенадцатую часть площади квадрата S2.