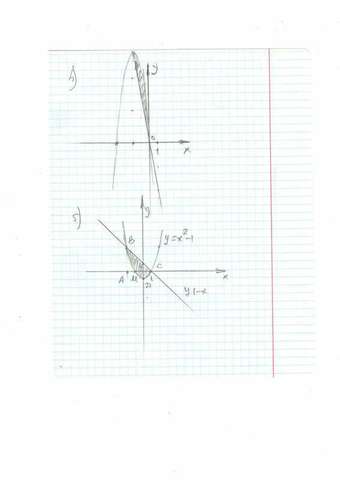
4) Смотрим на чертёж. Наша фигура - "линза", заключённая между прямой и параболой. Ищем границы интегрирования:
у = -6х
у = -12х -3х², ⇒ - 6х = -12х -3х², ⇒ 3х² + 6х = 0,⇒х(3х + 6) =0, ⇒
⇒х = 0 или х = - 2 . Это и есть границы интегрирования.
Фигура сверху ограничена параболой.Ищем площадь криволинейной трапеции( она "стоит" на оси х)
S₁ =₋₂∫⁰ (- 12x -3x²)dx = (-12x²/2 - 3x³/3) | в пределах от - 2 до 0 =
=(-6х² - х³)| в пределах от - 2 до 0 = 0 - ( -24 +8) = 16(ед²)
S₂ = SΔ = 1/2*2*12 = 12(ед²)
S abu/ = 16 - 12 = 4(ед²)
5)Смотрим и строим план действий:
а)ΔАВС. Найдём площадь.
б) криволинейный ΔАВМ .Его площадь надо будет вычесть.
в) Клочок МDC - его площадь надо будет прибавить.
Ну, с богом!
а) SΔABC = 1/2*2*3 = 3(ед.²)
б)₋₂∫⁻¹ (х² -1) dx = (x³/3 - x)| в пределах от -2 до -1 =
=-1/3 +1 - (-8/3 +2) = -1/3 +1 +8/3 - 2 = 4/3(ед²)
в)₋₁∫¹(х² +1) dx = (x³/3 - x)| в пределах от -1 до 1=
=1/3 -1 - (-1/3 +1) = 1/3 -1 +1/3 -1= 2/3 -2 = -1 1/3 = -4/3 ( минус показывает, что фигура под осью х. Для решения задачи берём модуль.
S фиг. = 3 - 4/3 +4/3 = 3(ед²)