1.
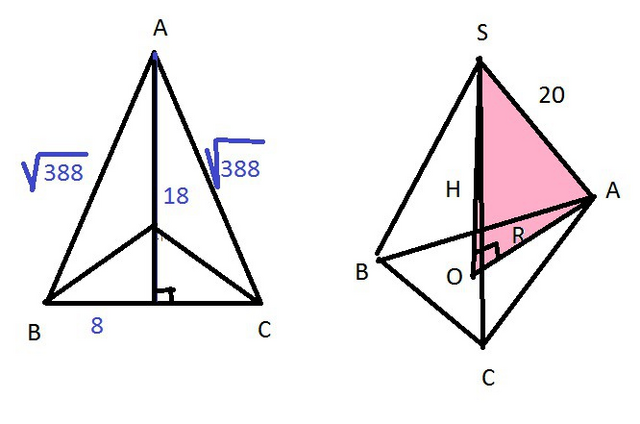
Все боковые ребра пирамиды равны, значит и проекции боковых ребер равны.
ОА=ОВ=ОС.
Точка О равноудалена от вершин треугольника АВС, значит
O- центр описанной около треугольника АВС окружности.
Найдем радиус окружности по формуле
R=abc/4S
S=(1/2)a*h
h=18
a=16
S=18*16/2=144
По теореме Пифагора
боковые стороны
b=c=√(8²+18²)=√388
R=16*√388*√388/(4*144)=97/9
По теореме Пифагора
H²=20²-R²=(400-(97/9)²)=32400-9409/81
H=√(22991)/9
2.
В основании пирамиды квадрат.
Пусть сторона квадрата равна а, площадь квадрата равна а².
a²=100
a=10
Боковые грани - равнобедренные треугольники с основанием 10, боковым ребром 13
По теореме Пифагора апофема пирамиды - высота равнобедренного треугольника
h²=13²-5²=169-25=144
h=2
S(бок)=4S(Δ)=4·10·12/2=240