У ривнобичну трапецію вписано коло радіусом 12см. Одна з бічних сторін точкою дотику...

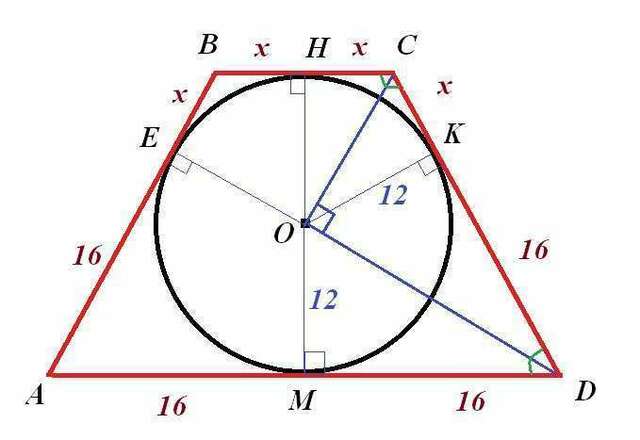
Чертеж к задаче во вложении.

Площаль трапеции $S=\frac{BC+AD}{2}HM$ .

Т.к. вписанная окружность касается всех сторон трапеции, и трапеция равнобедренная, то:

1) ОН⊥ВС, ОК⊥СД, ОМ⊥АД, ОЕ⊥АВ,

2) АВ=АМ=ДМ=ДК=16

3) ВЕ=ВН=СН=СК=х

По свойству окружности, вписанной в многоугольник, ее центр - это точка пересечения биссектрисс углов многоугольника. Значит, СО и ДО-биссектрисы двух односторонних углов. Как известно, биссектрисы двух односторонних углов взаимно перпендикулярны. Значит, ∆СОД-прямоугольный, в нём ОК - высота. Из подобия ∆ОКД и ∆ОКС следует равенство ОК²=СК·ОД

12²=16х

х=144:16=9

Значит, ВС=9+9=18.

Высота трапеции - отрезок НМ=12+12=24.

$S=\frac{18+32}{2}*24=600$ .

Ответ: 600.