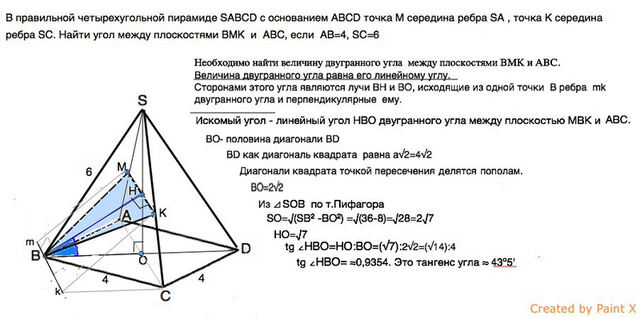
В правильной четырехугольной пирамиде SABCD с основанием ABCD точка М середина ребра SA, точка К середина ребра SC.
Найти угол между плоскостями BMK и ABC, если AB=4, SC=6.
Основание правильной четырехугольной пирамиды - квадрат, и вершина S пирамиды проецируется в точку пересечения O диагоналей квадрата АВСD.
Все ребра правильной пирамиды равны. Т.к. М и К делят противоположные ребра пополам, ВМ=ВК.
Основание МК треугольника МВК- средняя линия треугольника АSC и поэтому делит высоту SO пирамиды пополам. Пусть это будет точка Н.
Необходимо найти величину двугранного угла между плоскостями ВМК и АВС.
(Небольшое отступление: Плоскость, содержащая треугольник МВК, пересекается с плоскостью, содержащей ∆ АВС, по ребру mk. АС и mk параллельны, ВО⊥АС и mk. НВ⊥mk по т. о трех перпендикулярах.
Величина двугранного угла равна его линейному углу. Линейным углом двугранного угла называется угол, сторонами которого являются лучи, исходящие из одной точки ребра двугранного угла и перпендикулярные ему).
–––––––––––
Искомый угол - линейный угол НВО двугранного угла между плоскостью МВК и АВС.
ВО- половина диагонали ВD
BD как диагональ квадрата равна а√2=4√2
ВО=2√2
Из ⊿ SOB по т.Пифагора
SO=√(SB² -BO²) =√(36-8)=√28=2√7
НО=SO:2=√7
tg ∠НВО=НО:ВО=(√7):2√2=(√14):4
tg ∠НВО= ≈0,9354. Это тангенс угла ≈ 43º5'