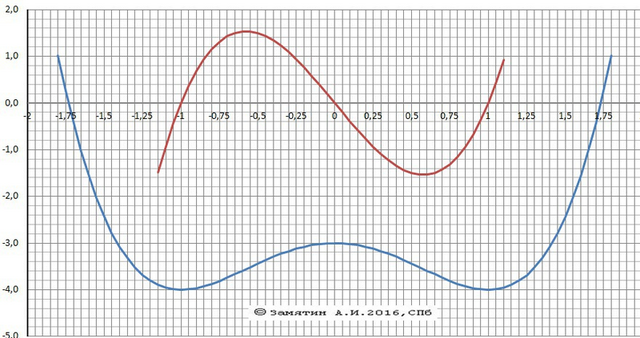
Функция Y = x⁴ - 2x² - 3.
График построен.
Исследуем.
Область определения - R - все действительные. разрывов нет.
Поиск экстремумов - находим производную - красный график.
Y' = 3x³ - 4x = x*(3x² - 4) = 0
Корни = х1 = 0 и х2 = √3/2 и х3 = - √3/2 ~ 0.87/
Убывает, когда производная отрицательная.
1) Х⊂(-∞;- √3/2] - убывает
2) Х= - √3/2 - минимум У =
3) Х⊂[-√3/2;0] - возрастает
4) Х= 0 - максимум У = -3
5) Х ⊂[0;√3/2] - убывает
6) Х = √3/2 - минимум У =
7) Х ⊂[ √3/2;+∞) - возрастает
Точки перегиба - вторая производная.
Y" =9*x² - 4 = 0
Корни - х1 = - 2/3 и х2 = 2/3.