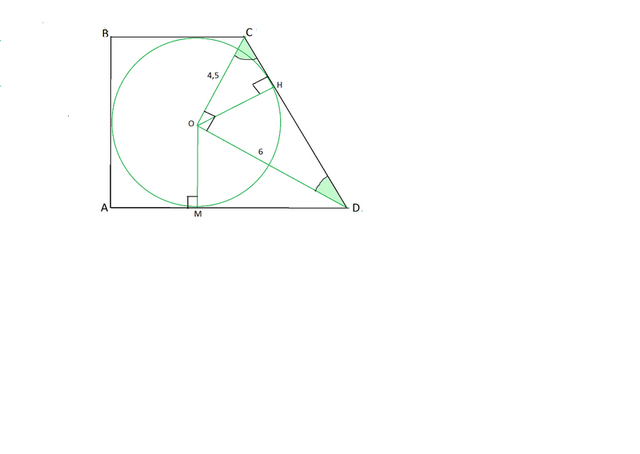
Сделаем по условию задачи рисунок.
В трапеции её боковая сторона видна из центра вписанной окружности
под углом 90°
( Углы при боковой стороне в сумме дают 180°, сумма их половин -90°, угол с вершиной при центре вписанной окружности =90°)
Следовательно, треугольник СОD - прямоугольный, и из него мы можем вычислить как саму боковую сторону СD, так и радиус СН вписанной окружности.
CD=√(4,5²+6²) =7,5
Для того, чтобы найти радиус ОН, нужно сначала найти любой отрезок боковой стороны.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
ОС²=СН*СD
20,25=СН*7,5
СН=2,7
Из прямоугольного треугольника СНО найдем радиус ОН вписанной окружности
ОН²=ОС²-СН²
ОН =√(20,25-7,29)=3,6
Так как трапеция по условию прямая,
АВ=2r=7,2
Вспомним, что в трапецию можно вписать окружность тогда и только тогда, когда сумма ее оснований равна сумме боковых сторон.
Отсюда
АD+ВС=CD+AB=7,5+7,2=14,7
Средняя линия трапеции равна полусумме оснований и равна
14,7:2=7,35
Ответ: 7,35