(8-х) (4х+9) < 0
32x+72-4x^2-9x<0<br>-4x^2+23x+72<0<br>1) f(x)=-4x^2+23x+72
2) Нули функции:
-4x^2+23x+72=0
D=23*23+4*72*4=529+1152=1681
√D=41
x1=(-23-41)/(2*(-4)=64/-8=-8
x2=(-23+41)/(2*(-4)=-2.25
3) Функция не существует - нет
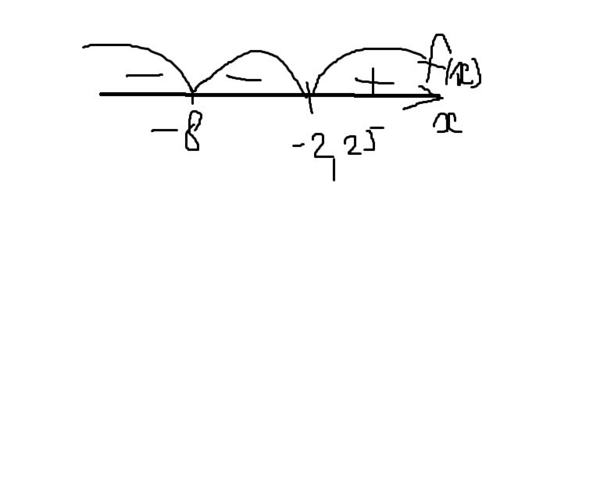
4) Методом интервалов
f(-10)="-"
f(-5)="-"
f(1)=" +"
(На картинке метод интервалов)
Ответ x∈(-бесконечности;-8)∪(-8;-2,25)
Или можно записать так (второй вариант ответа)
Ответ x∈(-бесконечности;-2,25) (Т.к. -8 можно включить сразу же в множество)
*Бесконечность - это 8, расположенная горизонтально