Умножим обе части уравнения на величину

, которая ни при каких

не обращается в
нуль. В результате получим равносильное уравнение:
![10^x*[( \frac{1}{6} )^x+( \frac{1}{8} )^x]=1 10^x*[( \frac{1}{6} )^x+( \frac{1}{8} )^x]=1](https://tex.z-dn.net/?f=10%5Ex%2A%5B%28+%5Cfrac%7B1%7D%7B6%7D+%29%5Ex%2B%28+%5Cfrac%7B1%7D%7B8%7D+%29%5Ex%5D%3D1)



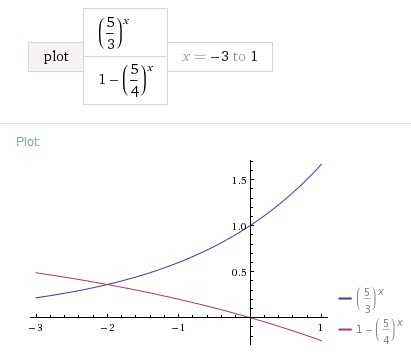
функционально-графический метод, легко заметить, что функция

монотонна растет на все области действительных чисел, а функция

монотонно убывает, что означает, что их графики пересекутся лишь в одной точке.
(левая и правая части уравнений - функции противоположных монотонностей)
Теперь, как стало известно, что решение существует одно, достаточно будет найти его любым способом вплоть до угадать.
По скольку

при любом действительном значении

, и по скольку

и легко видеть, что

проходит через начало координат, то искомый корень находится на промежутке отрицательных действительных чисел (отрицательный показатель заставит перевернутся дроби).
Т.е. пусть

, где

тогда:



нам нужно, что бы числители, к примеру, совпали.
на ум приходит пифагорская тройка:

для которой выполняется:

, т.е.

вот мы и угадали, что

тогда

Ответ: