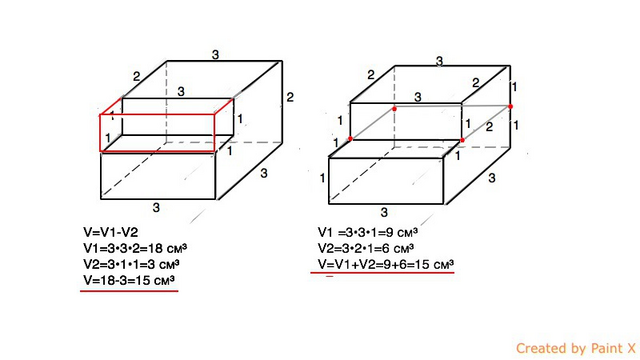
Задачи подобного рода можно решать двумя способами.
Так как дан многогранник, все двугранные углы которого прямые, то можно:
а) достроить данный многогранник до прямоугольного параллелепипеда с измерениями 3 см, 3 см, 2 см.
Тогда объем V данного многогранника будет равен объему V1 достроенного параллелепипеда без «пристройки», т.е. без объема V2 параллелепипеда с измерениями 3 см,1 см,1 см.
V=V1-V2
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
V1=3•3•2=18 см³
V2=3•1•1=3 см³
V=18-3=15 см³
б) разделить данный многогранник на два прямоугольных параллелепипеда
Тогда измерения нижнего (большего) будут 3 см, 3 см,1 см,
верхнего (меньшего) 3 см,2 см,1см
Соответственно объем большего V1 =3•3•1=9 см³
меньшего V2=3•2•1=6 см³
V=V1+V2=9+6=15 см³