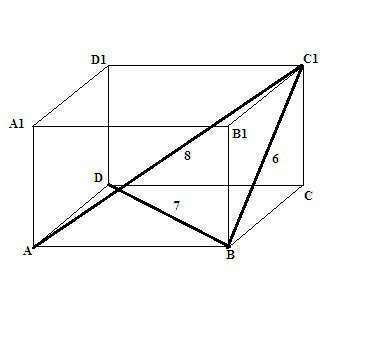
1) 1 рисунок.
У нас заданы три диагонали: AC1 = 8, BD = 7, BC1 = 6.
Заметим, что, поскольку ABCD - прямоугольник, то BD = AC = 7.
Получаем систему:
{ AC1^2 = AC^2 + CC1^2
{ BD^2 = AB^2 + BC^2
{ BC1^2 = BC^2 + CC1^2
Подставляем числа
{ 64 = 49 + CC1^2
{ 49 = AB^2 + BC^2
{ 36 = BC^2 + CC1^2
Решаем
{ CC1^2 = 64 - 49 = 15
{ BC^2 = 36 - CC1^2 = 36 - 15 = 21
{ AB^2 = 49 - BC^2 = 49 - 21 = 28
Получаем
{ CC1 = √15 = √3*√5
{ BC = √21 = √3*√7
{ AB = √28 = 2√7
Объем V = AB*BC*CC1 = 2√7*√3*√7*√3*√5 = 2*7*3*√5 = 42√5
2)
a) a = 11, b = 10, h = 12,
V = a*b*h = 11*10*12 = 1320
b) a = 3√2, b = √5, h = 10√10
V = a*b*h = 3√2*√5*10*√2*√5 = 3*10*2*5 = 300
3) Если диагональ грани куба AC = 14, то сторона
AB = AC/√2 = 14/√2 = 14√2/2 = 7√2
Его объем V = AB^3 = (7√2)^3 = 343*2√2 = 686√2
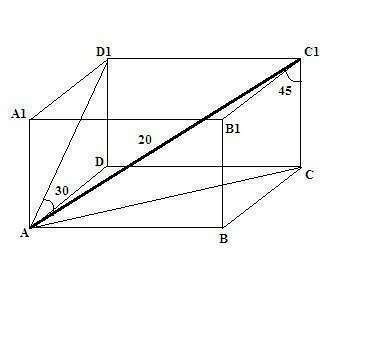
4) Рисунок 2
Треугольник AD1C1 - прямоугольный с углами 90, 30, 60.
Катет D1C1 против угла 30 гр. равен половине гипотенузы
D1C1 = AC1/2 = 20/2 = 10
Треугольник ACC1 - прямоугольный и равнобедренный
AC = CC1 = AC1/√2 = 20/√2 = 20√2/2 = 10√2
Треугольник ADC - тоже прямоугольный. По теореме Пифагора
AD^2 = AC^2 - CD^2 = 10^2*2 - 10^2 = 10^2
AD = 10
Объем V = AD*CD*CC1 = 10*10*10√2 = 1000√2
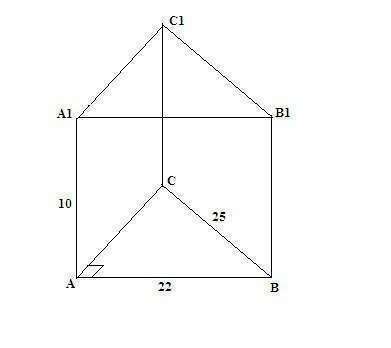
5) Рисунок 3.
По теореме Пифагора AC^2 = DC^2 - AB^2 = 25^2 - 22^2 = 625 - 484 = 141
Площадь основания равна половине произведения катетов
S = AB*AC/2 = 22*√141/2 = 11√141
Объем V = S*AA1 = 11√141*10 = 110√141
6)
a) Третья сторона основания по теореме косинусов равна
BC^2 = AB^2 + AC^2 - 2*AB*AC*cos BAC = 7^2 + 5^2 - 2*7*5*cos 60 =
= 49 + 25 - 2*35*1/2 = 74 - 35 = 39; BC = √39 < 7
Самая большая боковая грань - над стороной AC = 7, ее площадь равна 42,
значит, высота AA1 = 42/7 = 6.
Площадь основания S = 1/2*AB*AC*sin BAC = 1/2*7*5*sin 60 = 35/2*√3/2 = 35√3/4
Объем V = S*AA1 = 35√3/4*6 = 105√3/2
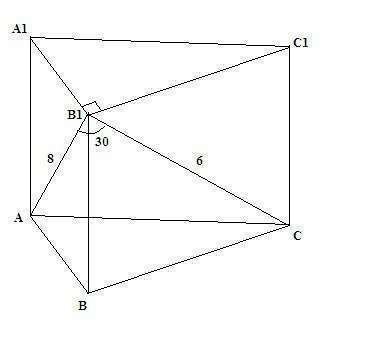
b) Рисунок 4.
По теореме косинусов
AC^2 = AB1^2 + CB1^2 - 2*AB1*CB1*cos AB1C = 8^2 + 6^2 - 2*8*6*cos 30 =
= 64 + 36 - 2*48√3/2 = 100 - 48√3
AC = √(100 - 48√3) = 2√(25 - 12√3)
Треугольники ABC, ABB1, BCB1 - прямоугольные. Получаем такую систему
{ AB^2 + BC^2 = AC^2 = 100 - 48√3
{ AB^2 + BB1^2 = AB1^2 = 64
{ BC^2 + BB1^2 = CB1^2 = 36
Сложив все три уравнения, мы получим
2AB^2 + 2BC^2 + 2BB1^2 = 100 - 48√3 + 64 + 36 = 200 - 48√3
AB^2 + BC^2 + BB1^2 = 100 - 24√3
Вычитая из этого уравнения каждое уравнение системы, получим:
BB1^2 = 24√3; BB1 = √(24√3) = 2√(6√3)
BC^2 = 36 - 24√3; BC = √(36 - 24√3) = 2√(9 - 6√3)
AB^2 = 64 - 24√3; AB = √(64 - 24√3) = 2√(16 - 6√3)
Площадь основания - прямоугольного треугольника АВС равна половине произведения катетов.
S = AB*BC/2 = 2√(9 - 6√3)*2√(16 - 6√3)/2 = 2√[(9 - 6√3)(16 - 6√3)]
Объем
V = S*BB1 = 2√[(9 - 6√3)(16 - 6√3)]*2√(6√3) = 4√[6√3(9 - 6√3)(16 - 6√3)]
Но на самом деле это неправильно, потому что где-то в задании опечатка.
Дело в том, что BC^2 = 36 - 24√3 < 0, а этого не может быть.