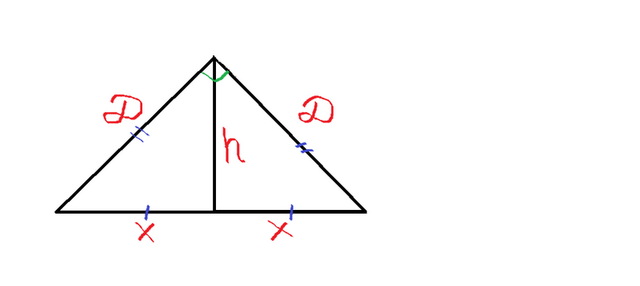
Так как две смежные диагонали перпендикулярны друг другу, получаем прямоугольный треугольник во вложении:
Тогда


Откуда получаем
Тогда получаем





Площадь боковой поверхности считаем по формуле: периметр основания на высоту:

Периметр равен:

Тогда площадь боковой поверхности будет равна: