Задача: Одна из диагоналей прямоугольной трапеции делит эту трапецию ** два прямоугольных...

Question

Задача: Одна из диагоналей прямоугольной трапеции делит эту трапецию на два прямоугольных равнобедренных треугольника. Какова площадь этой трапеции, если ее меньшая боковая сторона равна 4?

Answer 1

Трапеция АВСД. Угол В - прямой.

Диагональ АС образует с СД прмой угол. Треугольник АВС - прямоугольный равноберденный.
АВ=4, ВС=4 отсюда по теореме Пифагора АС=4 корней из 2. Но и СД равно 4 корней из 2. Значит, АД по теореме Пифагора равно 8.

Площадь трапеции равна полусумме оснований на высоту.

S=1/2*(4+8)*4 = 24

Answer 2

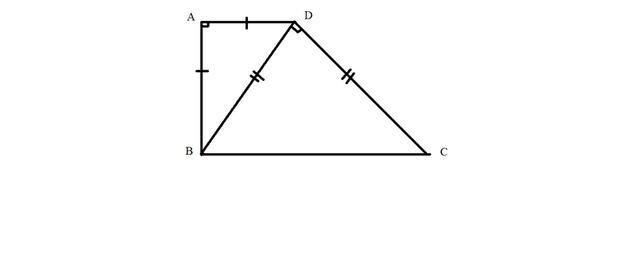
Боковая сторона (АВ)=4. Так как треугольник равнобедренный, то AD=4 тоже. По теореме Пифагора получаем, что ВD=корню из 32. Рассмотрим треугольник BDC. Он тоже равнобедренный, причем катеты равны корню из 32. Найдем гипотенузу, которая является большим основанием в трапеции. По теореме Пифагора она равна 8.

Осталось только посчитать площадь. S=h*0,5*(a+b), где a, b - основания, h - высота в трапеции, равная меньшей боковой стороне (трапеция прямоугольная). S=0,5*4*(4+8)=24

Ответ: S=24

---