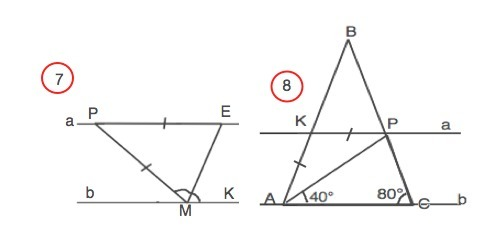
По рис. 7.
В треугольнике МВЕ стороны РЕ=РМ. Следовательно, он равнобедренный, и углы при основании МЕ равны. Отметим справа от т.М точку К (для удобства записи).
МЕ - биссектриса угла РМК и делит его на два и оба равны углу РЕМ.
∠РЕМ=∠ЕМК, а они – накрестлежащие. Равенство накрестлежащих углов - признак параллельности прямых. ⇒ а и b- параллельны.
По рис. 8.
Сумма углов треугольника 180°. ⇒ ∠АРС=180°-(40°+80°)=60°
Треугольник АКР равнобедренный ( дано).
∠КРА=∠КАР. Так как по условию АВ=ВС, ∠ВАС=∠ВСА=80° ( как угол при основании равнобедренного треугольника).
Тогда ∠КАР=80°-40°=40°.
∠КРА=∠КАР=40° и равен накрестлежащему углу РАС.
Равенство накрестлежащих углов - признак параллельности прямых. ⇒ прямые a и b параллельны.