Заметим, что неравенство не меняется при замене (x, y) на (y, x), поэтому фигура симметрична относительно прямой y = x.
Кроме того, неравенство не меняет вид и при замене (x, y) на (-y, -x), поэтому фигура симметрична относительно прямой y = -x.
Вся плоскость разбивается прямыми y = x, y = -x на четыре области; мы имеем право решить неравенство в любой из них, получить часть фигуры, а затем путём отражений достроить всю фигуру целиком.
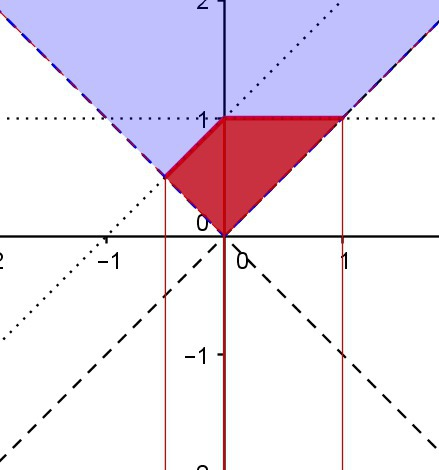
Я буду решать неравенство в "верхней четверти", т.е. в области y ≥ |x|. В ней |y| = y, |x - y| = y - x.
1) Пусть x < 0, тогда |x| = -x, и неравенство примет вид
-x + y + y - x ≤ 2
2y - 2x ≤ 2
y ≤ x + 1
2) Если x ≥ 0, то |x| = x и неравенство упрощается:
x + y + y - x ≤ 2
2y ≤ 2
y ≤ 1
Строим и получаем то, что изображено на первом рисунке.
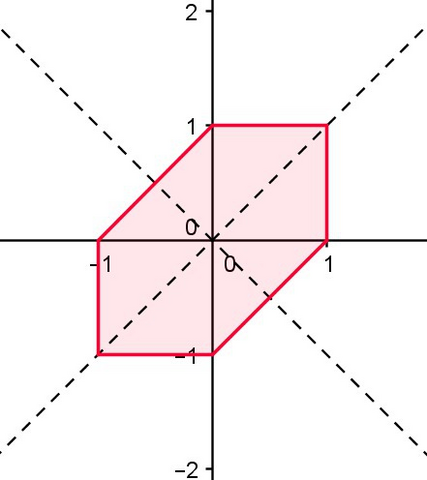
После отражений получим квадрат со стороной 2 с двумя отрезанными углами. Его площадь равна 4 - 1 = 3.