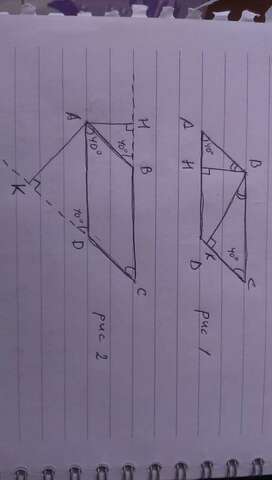
Сначала найдём углы параллелограмма: пусть острый угол будет 2х, а тупой 7х, тогда
2х + 7х = 180
9х =180
х = 20
Значит острый угол 40°, а тупой 140°.
1) (рис 1)
угол АВН = КВС = 180°-90°-40°=50°
угол НВD (искомый) = угол АВС - АВН - КВС = 140°-50°-50°=40°
Ответ: 40°.
2) (рис 2)
угол НВА = АDК = 180°-140°=40°
Тогда угол ВАН = КАD = 180°-90°-40°=50°
Значит угол НАК (искомый)= ВАD+ВАН+КАD = 40°+50°+50°=140°
Ответ: 140°.