Медианы пересекаются в одной точке, которая делит их в отношении 2:1, считая от вершины.
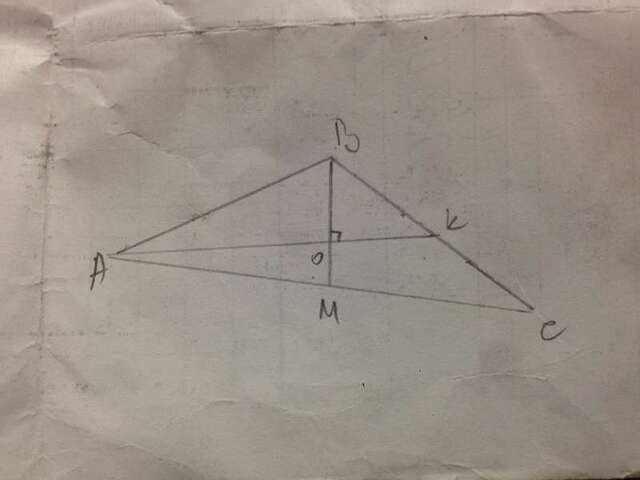
В тр-ке АВС медианы АК и ВМ пересекаются в точке О. ВС=6 см, АС= 8 см.
Пусть КО=х, МО=у, тогда АО=2х, ВО=2у.
В тр-ке ВОК ВК²=ВО²+КО²,
3²=4у²+х².
В тр-ке АОМ АМ²=АО²+МО²,
4²=4х²+у² ⇒ у²=16-4х², подставим в уравнение выше:
3²=4(16-4х²)+х²,
9=64-16х²+х²,
15х²=55,
х²=11/3.
у²=16-4·11/3=4/3.
АО²=(2х)²=4х², ВО=4у².
В тр-ке АВО АВ²=АО²+ВО²=44/3+16/3=60/3=20.
АВ=√20=2√5 см - это ответ.