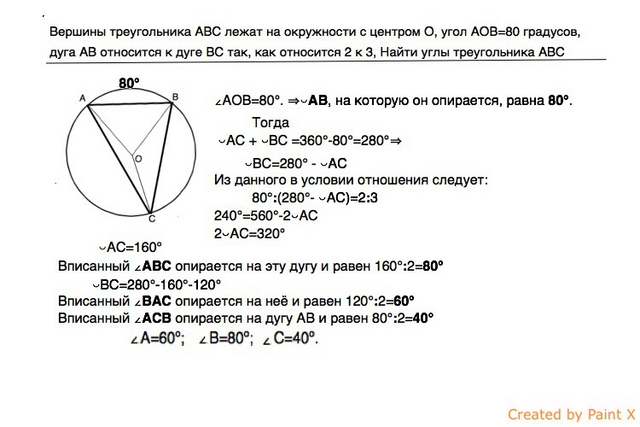
Вершины треугольника АВС лежат на окружности с центром О, угол АОВ=80º, дуга АВ относится к дуге ВС так, как относится 2 к 3.
Найти углы треугольника АВС
В подобных задачах обычно дается отношение ◡АС
: ◡ВС, здесь дано отношение известной дуги AB к неизвестной ВС, причем о второй неизвестной
◡АС ничего не сказано.
Решение.
Центральный ∠АОВ=80°. ⇒
◡АВ, на которую он опирается, равна 80°.
Тогда
◡АС +
◡ВС =360°-80°=280°⇒
◡ВС=280° -
◡АС
Из данного в условии отношения следует:
80°
:(280°-
◡АС=2:3
240°=560°- 2
◡АС
2
◡АС=320°
◡АС=160°
Вписанный
∠АВС опирается на эту дугу и равен 160°
:2=
80°
◡ВС=280°
-160°
-120°
Вписанный
∠ВАС опирается на неё и равен 120°
:2=
60°
Вписанный
∠АСВ опирается на дугу АВ и равен 80°
:2=
40°
Сумма углов ∆ АВС=80°+60°+40°=180
°
АВ
:ВС=80°
:120
°=
2:3